Hyungmin Kim

AI모델을 실 생활 속으로.

[논문공부] colorization transformer

Colorization Transformer

오늘 읽은 논문은

Manoj Kumar et al., “Colorization Transformer”, ICLR, 2021 이다.

Image colorization 및 생성 모델 관련 논문은 처음 보는 것이라 더 열심히 보아야 겠다.

title

1. 논문의 개요

최근 Automated Image Colorization 방법들은 log-likelihood estimation에 기반한 neural generative approach가 대부분임.

1.1 Neural generative approach-based Image Colorization Methods

아래 소개된 논문들은 나중에 더 자세히 공부할 예정 우선은 메인 컨셉만 확인.

요즘 Colorization model은 probabilistic한 방법을 사용하기 때문에 아래 논문을 추가적으로 살펴봄.

  • Amelie Royer et al. “Probabilistic Image Colorization”, BMVC, 2017

    Pixel-CNN, Pixel-CNN++ 등에 영향을 받은 방법론.

    lab_img_space <Figure 2.> Lab image space [출처]

    LAB image space 라고 가정했을 때, 우리는 흑백 영상의 분포를 알고 있으므로, 학습 샘플들로 Conditional distribusion 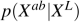eq001 를 모델링 하는것이 목표.

    Conditional distribusion 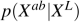eq001를 구하려면,

    $X^L$은 given이고, GT($X^{ab}$)도 아니까 모델을 찾을수 있다는 말이고 모델을 찾기 위해서 Conditional distribution을 정의함.

    여기서는 $X^{ab}$의 픽셀 값을 이전 연구처럼 deterministic 하게 추정하지 않고 샘플링하는데, 즉 VAE 처럼 일단 파라미터라이제이션 하고 hidden에서 샘플링하는데, 이때 softmax로 0~255 사이의 값(8bit)을 뽑는다. continual이 아니기 때문에 log-likelihood estimation은 멀티누이 분포를 가정하고 했다는 말이다.

    Conditional distribution을 구할때는,

    각 픽셀별로 n개의 픽셀(시행)에 대해서 조건부 확률의 연쇄법칙(Chain rule for conditional probability)에 의해서

    L 채널에서 a,b 채널로의 조건부 확률을 다음과 같이 나타낼 수 있다.

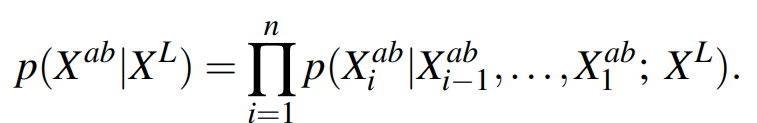
    conditional_probablilty_of_Lchannel_to_ab_chnnel

    테스트 시에는? 픽셀 순으로 sequantial 하게 진행.

    먼저 입력된 $X_L$ 있으므로 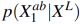x_1_variable를 앞서 학습한 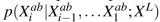conditional_probability_of_Lchannel_to_ab_channel 로부터 샘플링. 이후에도 연속적으로 모든 픽셀에 대해서 동일한 과정을 수행.

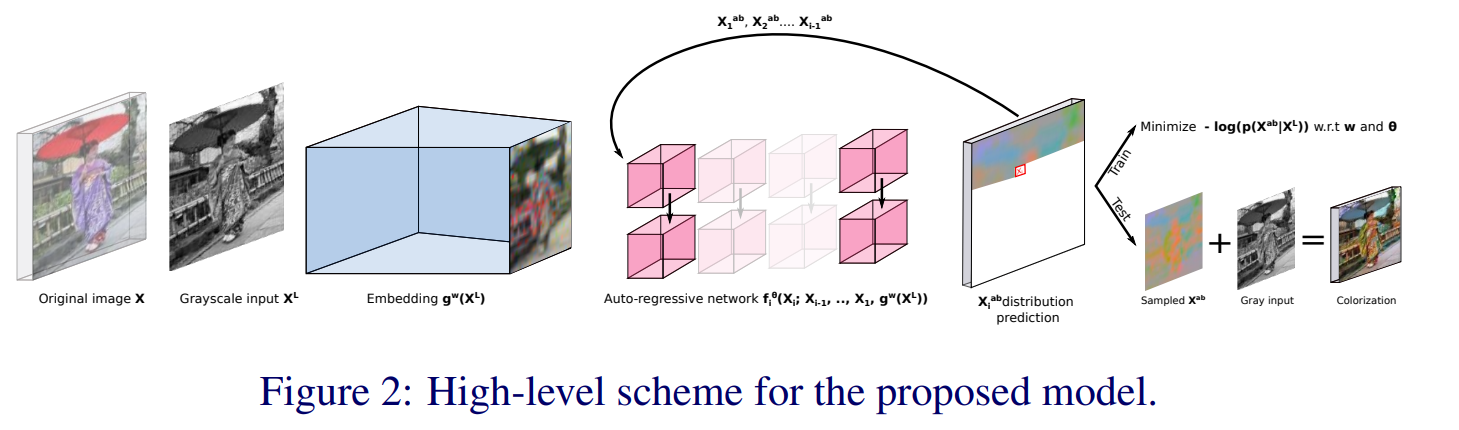    probabilistic_colorization <Figure 3.> Probabilistic Colorization.

    전체 네트워크는 enbedding network $g^w$와 autoregressive network $f^\theta$로 이루어져 있다.

    embedding netowrk $g^w$는 일반적인 CNN이고, 핵심은 autoregressive network $f^\theta$이다. 이건 PixelCNN++이다.

    PixelCNN 원 논문을 살펴보면,

    “The basic idea of the architecture is to use autoregressive connections to model images pixel by pixel, decomposing the joint image distribution as a product of conditions”

    pixelcnn

    커널 안에서 다음 생성될 픽셀에 대해서, 0~255 사이의 값(8bit)로 softmax prediction 수행.

    그러니까 일단 $g^w$로 파라미터라이제이션 하고 샘플링을 픽셀 by 픽셀로 연속적으로 해서 0~256사이의 값을 가지게 추정하고

    Maximum likelihood를 향해 학습(negative loglikelihood minimization) 하겠다는것 같다.

    그걸 다음 픽셀을 생성하면서 sequantial하게 연속적으로 conditional distribution을 정의하면서 말이다.

    crossentrophy loss 최적화 한다고 했으니 확률분포는 멀티누이 분포(Multinoulii distribution)를 가정했다는 말이겠고요.

    그런 식으로!!! 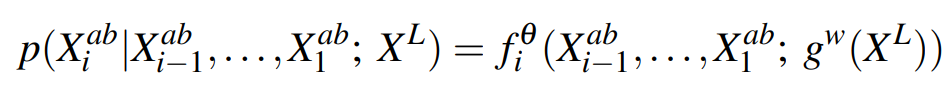eq06 $X^L$ 로부터 $X^{ab}$를 prediction 한다.

    그거를 굳이 수식으로 쓰면 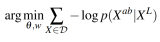eq07 이렇게 된다.

    그래서 논문에서 “The current state-of-the-art in automated colorization are neural generative approaches based on log-likelihood estimation” 라고 한것 같다.

    원리는 동일한데, PixelCNN+는 나중에 더 봐야할듯.

    일단 Colorization transformer에서는 PixelCNN이 아니라 PixelCNN+를 사용하긴 했는데, 개념은 비슷하니 다음에 본 논문 다루어볼때 하기로 하고 이쯤 넘어가자…

    다음에 이 논문도 리뷰 해야 할듯.

방금 전 본 것 처럼, 최근 colorization 방법들은 대부분 probabilistic model. 이전 deterministic 한 방법보다 장점있어서 널리 적용됨.

1.2 Colorization Transformer

Colorization Transformer(ColTran)도 앞서 간단히 살펴본 probabilistic corolization 모델이다.

Transformer 구조이며 axial self-attention block으로 transformer 구성.

axial self-attention block의 장점은 global receptive field를 저렴한 비용으로 얻을 수 있다는 점이다.(자세한 이야기 논문참조)

한번에 high resolution의 gray-scale 영상을 colorization하는 것은 어렵고 연산량도 많기 때문에, 3개의 하위 sub task로 분리.

  • Coarse low resolution aotoregressive solorization

  • parallel colorsuper-resolution

  • spatial super-resolution

한번에 colorization 하기 힘드니 low resolution으로 먼저 하고 super resolution한다는 뜻.

2. Background: Axial Transformer

그렇다 이 논문을 보기 전에 또 Axial Trnasformer를 알아야한다.

Axial transformer는 각 row 및 column 단위로 어텐션을 한다는 점에서 생성할 픽셀들을 연속적으로 생성하는 Image colorization에 적합한 방식이라 생각해서 사용된것 같다.

3.1 Row and Column self-attention

Criss-Cross Attention(Axial Attention)

Zilong Huang et al. “CCNet:Criss-Cross Attention for Semantic Segmentatioin”, 2020

Axial transformer는 Criss-Cross 네트워크에 영감을 받아 시작되었다.

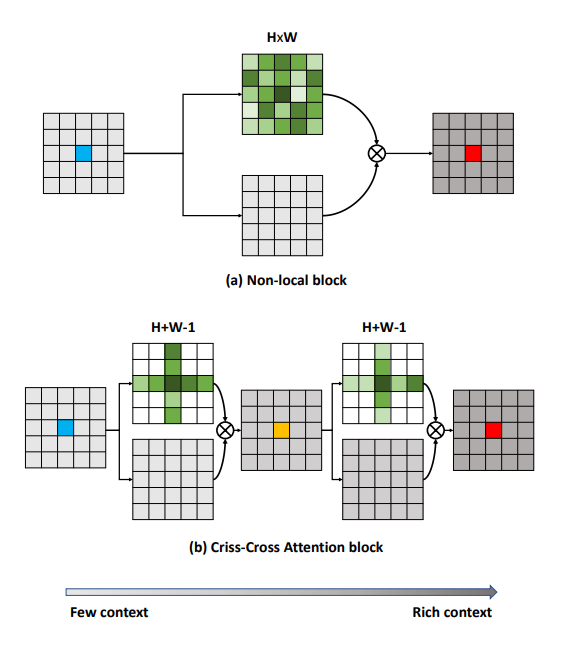
crisscross

그 개념은 원래 FCN(Fully Convolutional Network)에서 (컨볼루션 기반의 고질적인 특징인) short-range receptive field만을 가지게 되는 한계점을 극복하기 위해 등장했다.

이를 극복하기 위한 방법은 non-local 모듈과 같이 attention을 이용해 모든 픽셀을 densely aggregation 하는 것이다.

그러나 이는 attention map을 모든 픽셀 끼리 연산해야 하기 때문에 연산 복잡도가 굉장히 크다 (O($N^2$))

(CCNet 논문에서는 이를 픽셀들을 node로 본 GNN(Graph Neural Network) 형태라고 설명)

semantic segmentation과 같은 high resolution feature가 필요한 분야에서는 이는 좋지 않다.

전체 픽셀로 attention map을 생성하지 않고 horizontal, vertical 방향(각 픽셀이 속한 column, row)에 대해서 연속적으로 attention.

crisscross2

self-attention이므로 QKV 생성을 한다.

  • 먼저 linear projection(1x1 Convolution)을 통해 Q, K, V 생성. (C’는 dimension reduction시 감소된 차원. 아닐경우 입력과 동일)

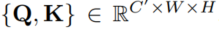
crisscross3

spatial dimension은 동일하다.(어텐션 맵을 생성해야 하니)

  • Affinity Operation

Criss-cross attention의 핵심 연산이라고 볼 수 있음. 어텐션 맵

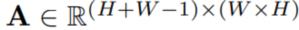crisscross4 를 생성.

어떤식으로 하나 궁금해서 공식 torch 구현의 forward 부분만을 가져옴

def forward(self, x):
   m_batchsize, _, height, width = x.size()
   proj_query = self.query_conv(x)
   proj_query_H = proj_query.permute(0,3,1,2).contiguous().view(m_batchsize*width,-1,height).permute(0, 2, 1)
   proj_query_W = proj_query.permute(0,2,1,3).contiguous().view(m_batchsize*height,-1,width).permute(0, 2, 1)
   proj_key = self.key_conv(x)
   proj_key_H = proj_key.permute(0,3,1,2).contiguous().view(m_batchsize*width,-1,height)
   proj_key_W = proj_key.permute(0,2,1,3).contiguous().view(m_batchsize*height,-1,width)
   proj_value = self.value_conv(x)
   proj_value_H = proj_value.permute(0,3,1,2).contiguous().view(m_batchsize*width,-1,height)
   proj_value_W = proj_value.permute(0,2,1,3).contiguous().view(m_batchsize*height,-1,width)
   energy_H = (torch.bmm(proj_query_H, proj_key_H)+self.INF(m_batchsize, height, width)).view(m_batchsize,width,height,height).permute(0,2,1,3)
   energy_W = torch.bmm(proj_query_W, proj_key_W).view(m_batchsize,height,width,width)
   concate = self.softmax(torch.cat([energy_H, energy_W], 3))

   att_H = concate[:,:,:,0:height].permute(0,2,1,3).contiguous().view(m_batchsize*width,height,height)
   att_W = concate[:,:,:,height:height+width].contiguous().view(m_batchsize*height,width,width)
   out_H = torch.bmm(proj_value_H, att_H.permute(0, 2, 1)).view(m_batchsize,width,-1,height).permute(0,2,3,1)
   out_W = torch.bmm(proj_value_W, att_W.permute(0, 2, 1)).view(m_batchsize,height,-1,width).permute(0,2,1,3)
   return self.gamma*(out_H + out_W) + x

[BW, H, C’], [BH, W, C’] 와 같이 reshaping 한다음에 bmm하는식으로 접근한다.

bmm

crisscross01

crisscross02

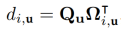
그려보면 이런식이라고 보면 된다.

Axial Transformer

유용한 참고자료

개인 프로젝트

맨 위로 이동 ↑

논문 공부

맨 위로 이동 ↑